Ez a feladat szerepelt a 2006-os őszi csapatversenyen.


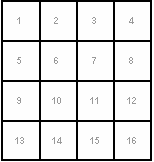
A fenti ábra szerint egy 4×4 hosszú kocka rajzát 1 hosszú pálcikákból raktuk ki, összesen 40 darabból. Az ábrán a pálcikák állásán nem változtathatunk, de lehetőségünk van arra, hogy egy-egy darabot elvegyünk, ezzel változtatva az ábrán.
Vegyünk el pálcikákat úgy, hogy egyetlen (1×1, 2×2, 3×3, vagy 4×4 méretű) négyzet se maradjon!
Minden pálcikának e jele a következőképp alakul: azon négyzet száma, amellyel határos, illetve a hozzá tartozó égtáj betűjele (észak – é, kelet – k, dél – d, nyugat –n). Így például a négyzet tetején lévő pálcikák rendre: 1é, 2é, 3é, 4é. Bizonyos pálcikákat két különböző kóddal is azonosíthatunk (pl. 5k és 6n), ilyenkor bármelyik kód megfelelő.

Legalább hány pálcikát kell elvennünk a feladat teljesítéséhez?
(5 pont)

Melyek ezek? (Adjuk meg a pálcikákat a kódjukkal!)
(5 pont)

Kevesebb miért nem elég? (Bizonyítással.)
(5 pont)